Pythagoras for Knitters
... or how a little knowledge of Geometry can be a Good Thing, especially for Stash-Busters... Recently, I was doing a spot of stash-busting, and I decided to knit my sister a little shawl from some ribbon-y yarn in my stash. It's a straightforward matter to knit a triangular shawl, especially in garter stitch, and we probably all know how it's done ... cast on 2 stitches, and knit them, then on each following row, increase one stitch at the beginning of the row, usually by knit 1, knit 1 tbl, then knit to the end of the row. When the resulting triangle is big enough for what we want, we cast off. So far, not very difficult ... but how do we know if we have enough yarn for what we want to do? And that's when Geometry can be our Best Friend ... I had four balls of Veritas 'Colorado' (bought in Veritas in Mons, Belgium), that's this stuff here:

No yardage on the ball band, though I would guess it was around about the $50\cdot60$ yard mark, it's a type of slightly glittery 'railroad'- type ribbon, with little tufts along the edges, and when knitted up in garter stitch, it looks rather like the picture overleaf - quite a 'crunchy', springy texture Article - "Pythagoras for Knitters" $\copyright$ - Mary-Lou Quick (MLQKnits), 2008 Blog:http://mlqknits.typepad.com/odd_ball_knitting/ Website: http: / /www.mlqknits.com/

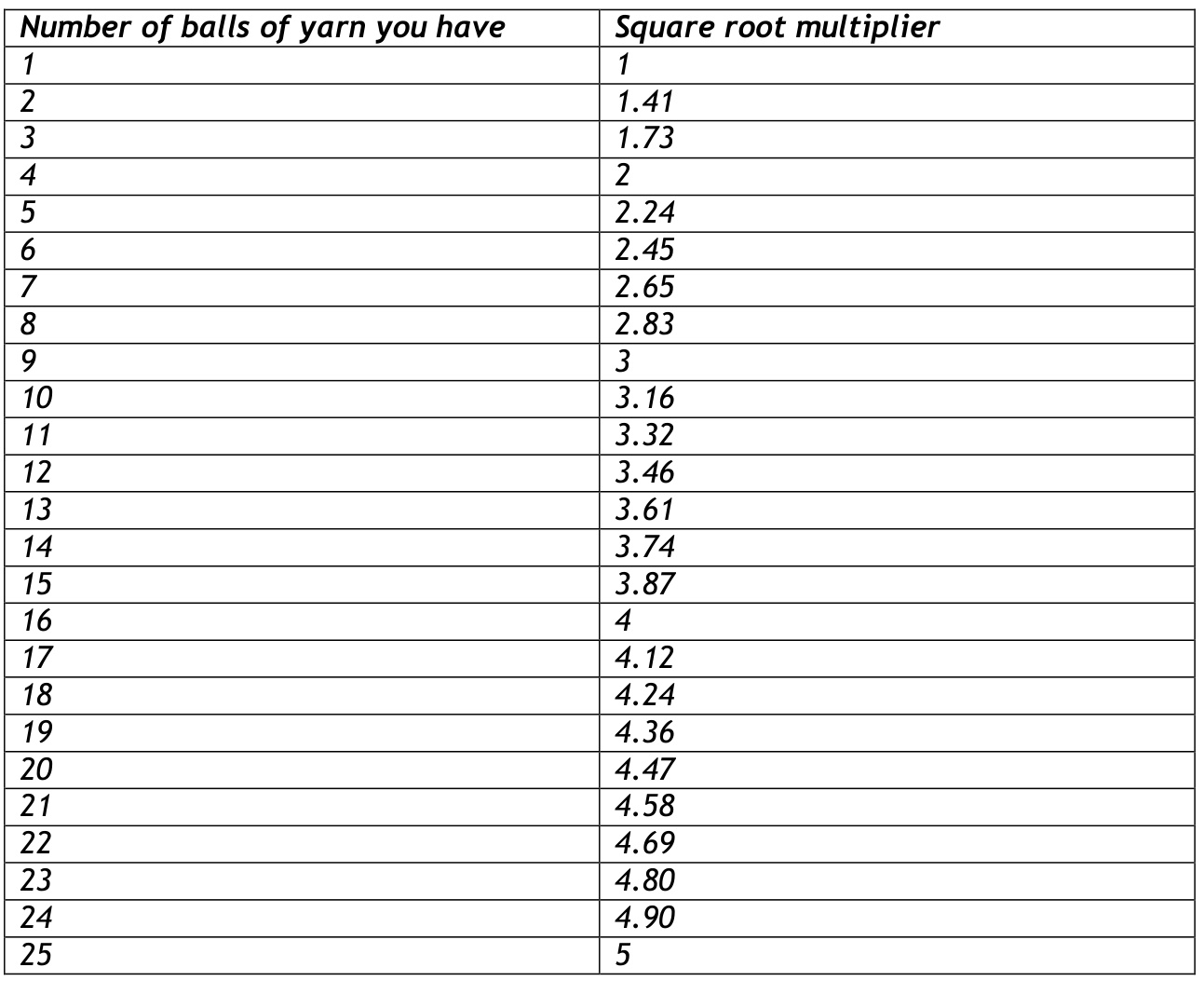
I had originally intended to knit a scarf with it, but decided to be a bit cleverer ... hence the shawl, but I wasn't really sure just how far the 240 yards would go, and I didn't want to end up with something too small to be of any use. Enter Pythagoras, and one of the only two formulas that most people know (the other one is $\scriptstyle\mathtt{e=m c^{\wedge}2}$ ! Knitting the shawl in the way I've described gives you an isosceles triangle (two sides the same length, two angles the same), but more importantly, the angle between the two short sides is a right angle, like this
Article - "Pythagoras for Knitters"
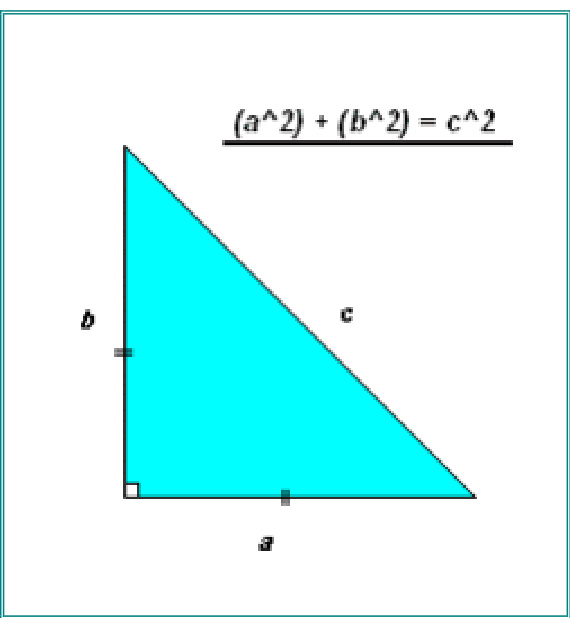
$\copyright$ - Mary-Lou Quick (MLQKnits), 2008 Blog:http://mlqknits.typepad.com/odd_ball_knitting/ Website: http://www.mlqknits.com/ and once I knew how big a triangle one ball would make (12 inches on each of the short sides and about 17 inches on the long side), it was a relatively simple matter to work out that 4 balls would give me a triangle twice as long on each side (ie 24 inches for each short side, and about 34 inches on the long side), like this
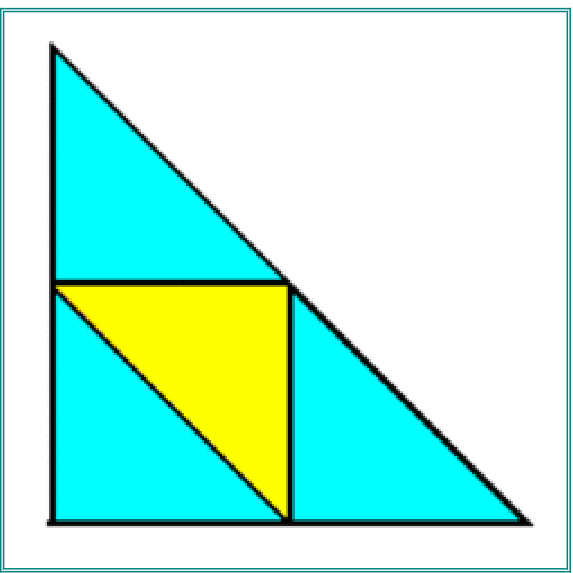
Each right-angled triangle in the diagram represents one ball of yarn. I've coloured them so you can see clearly how they all fit together Interestingly, to make that triangle three times as long on every side as the original, you need9 balls of yarn
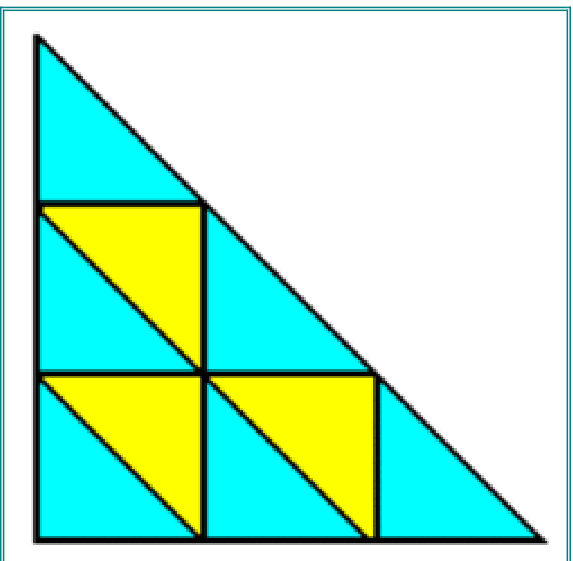
... I will leave it to you to work out how many balls you need to knit a triangle 4 or 5 times as long on each side, but here's the sequence - 1 4, 9, ..,... - see if you can fill in the missing numbers - and no, there is no prize for this (just a sense of satisfaction). That's all well and good, but what if Id had only 2, 3 or 5 balls (or some other number of balls of yarn not in that sequence?) Thanks to knowing a bit about right-angled triangles and their properties, I can work that out too, based on the dimensions of a triangle made from one ball of yarn, with the aid of a calculator that can do square roots, or using MsExcel. And just so that you can do it too - here's how: Use your calculator to find out the square root of the number of balls you have, eg. the square root of two is a nasty number that goes on for ever, but the first few digits are 1.414213562 (in case you're interested, this type of number is called an irrational number), but you can round it to something more reasonable, say 1.41 (to 2 decimal places). Now multiply the sides of the triangle you get from 1 ball of yarn by 1.41, (ie. if the sides from 1 ball are 10 inches, 10 inches, and 14.14 inches, then 2 balls will make a triangle with sides 14.14 inches, 14.14 inches and 20 inches). If you want to do the same thing in Excel, type this formula into the first cell (cell A1) in the top left corner of the spreadsheet,'=sqrt(x)' (leave out the quote marks, and replace x with the number of balls of yarn you have). That gives you the multiplier you need. Now type into another cell'=A1\*y' where y is the length of one of the two short sides of the original triangle, and hit enter. Do the same sort of thing in another cell for the long side of the triangle, and now you know how big your finished triangle will be. And so to the pattern itself: 4 balls Veritas Colorado (between 200 - 300 yards of aran weight ribbon yarn) 2 balls of Zettl Cotton-Classic Cable DK (200 yards of Cotton DK) A pair of 6mm needles A 4.5 - 5mm crochet hook Note that crochet terminology is English. US terms are given in brackets. Also note that tension is not teribly important for this piece, though ilt should be loose to allow for the springiness of the yarn, so although the recommended needles given for Veritas Colorado are 4.5 - 5mm, I opted to use 6mm to give it a bit of drape. With ribbon yarn, and 6mm needles, cast on 2 stitches by the e-wrap method Row 1: Knit Row 2: (K1, K1tbl) in the first stitch, K1 - (3 stitches) Row 3: (K1, K1tbl) in the first stitch, K to end - (4 stitches) Repeat Row 3 till you have 10 stitches altogether Nexr Row: K5, yo, K5 - (11 stitches) Next Row: K5, yo, K1, yo, K5 - (13 stitches) Next Row: K5, yo, K3, yo, K5 - (15 stitches) Continue in this way working 2 more stitches each time between the yo's until you have just enough yarn to cast off. Cast off loosely. Now work the edging: With crochet hook, and cotton DK, starting from the cast off edge, work 1 dc (Us, work 1 sc) into each cast off stitch across the cast off edge, then work 1 dc (US, work 1 sc) into each garter ridge along each of the 2 short sides. Join to the first dc with a slip stitch. Turn. (the remainder of the edging will only be worked along the short sides) $1^{\mathrm{st}}$ Row: $^{*}\mathsf{C h}\;5$ , skip 3 dc, dc into next $\mathsf{d}\mathsf{c}^{*}$ , repeat to last 3 dc before corner, (ch 5, skip 3 dc, dc into corner) twice, $^{*}\mathsf{c h}\;5$ , skip 3 dc, dc into next $\mathsf{d}\mathsf{c}^{*}$ ,repeat to end.Turn. (Us: $^{*}\!C h$ 5, skip 3 sc, sc into next $s c^{*}$ ,repeat to last 3 sc before corner, (ch 5, skip 3 sc, sc into corner) twice, \*ch 5, skip 3 sc, sc into next $s c^{*}$ , repeat to end. Turn.) Article - "Pythagoras for Knitters" $\copyright$ - Mary-Lou Quick (MLQKnits), 2008 Blog:http://mlqknits.typepad.com/odd_ball_knitting/ Website: http: / /www.mlqknits.com/ $2^{\mathsf{n d}}$ Row: Ch 5, dc in first ch-sp,\*ch 5, dc in next ch $\boldsymbol{\mathsf{S}}\boldsymbol{\mathsf{p}}^{*}$ , repeat to corner ch-sp, work additional ch 5, dc in corner space, \*ch 5, dc in next ch $\boldsymbol{\cdot}\boldsymbol{\mathsf{s p}}^{*}$ ,repeat to last ch-sp, ch 3, dc in last dc. Turn. (Us, Ch 5, sc in first ch-sp, \*ch 5, sc in next ch $s p^{*}$ , repeat to corner ch-sp, work aditional ch5, sc in corner space, \*ch 5, sc in next ch $\boldsymbol{s p}^{*}$ , repeat to last ch $\cdot s p$ , ch 3, sc in last sc. Turn.) Repeat $2^{\mathsf{n d}}$ row once more. Make a fringe from 8 inch lengths of cotton DK. Knot lengths using double hitch knot with 2 lengths of fringe through each chain space. Trim fringe if necessary, and darn in any loose ends of yarn. $\copyright$ - Mary-Lou Quick (MLQKnits), 2008 Blog:http://mlqknits.typepad.com/odd_ball_knitting/ Website: http: / /www.mlqknits.com/ NB - It occurs to me that some people don't have access to either the right kind of calculator, or Ms-Excel, so just for you, here are the square roots for the numbers 1 - 25 (where these are irrational, I've simplified them to 2 decimal place which should be quite sufficient for most purposes)